Location: Seminar Room of the IMUS (see Section "How to come ?" at the end of this page)

Start: Tuesday March 11th at 9:30

Finish: Friday March 14th at 14:00

This workshop gathers researchers working in the fields of modelling and design of numerical methods linked to some aspects of the simulation of avalanches. It is organized in the framework of the French ANR's research thinktank (ARP) MathsInTerre and the "Mathematics of Planet Earth" (MPE) initiative.

The themes of the conference will focus particularly on:

• modelling of viscoplastic materials,
• debris flows modelling,
• new numerical methods adapted to these models.

The goal is to maximize discussions and interdisciplinary exchanges between physicists and mathematicians, and to produce a prospective synthesis for MathsInTerre which can be found here.

List of Speakers:

Christophe ANCEY (EPFL, Switzerland)

Patricio BOHORQUEZ (University of Jaen, Spain)

François BOUCHUT (CNRS & University of Paris-Est, France)

Manuel J. CASTRO (University of Malaga, Spain)

Yoël FORTERRE (CNRS & University of Marseille, France)

Daniel LE ROUX (University of Lyon, France)

Anne MANGENEY (IPGP, France)

Guillaume OVARLEZ (CNRS & IFSTTAR, France)

Vladimir SHELUKHIN (Lavrentyev Institute of Hydrodynamics, Russia)

Paul VIGNEAUX (ENS de Lyon, France)

Scientific organization: Didier Bresch (CNRS, France), Enrique D. Fernández-Nieto (University of Seville, Spain), Paul Vigneaux (ENS de Lyon, France)

Administrative support: Emilie Neveu, Marjorie Stievenart-Ammour (IHP)

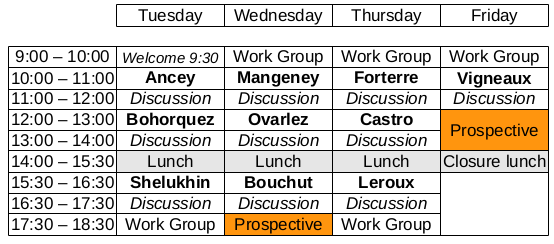
Tentative planning: see Titles and Abstracts below on this page

The workshop is also supported logistically by the Institute of Mathematics of Seville (IMUS) and the Departamento de Matemática Aplicada I (US).

 _____________________________________________________________________

Titles & Abstracts

Christophe ANCEY

Avalanche of fluid in the laboratory: the dam-break problem revisited

In fluid mechanics, the dambreak problem refers to the gravity-driven flow of a fixed volume of fluid suddenly released. The problem is not only of great importance to ensuring safety of manmade and natural dams, but also to understanding the dynamics of time-dependent free-surface flows. Considerable attention has been paid to this fundamental problem since Ritter worked out the earliest solution to the dambreak problem for inviscid fluids in 1892. In particular, many experiments were carried out to measure the flow depth profiles and front position for various settings. Until very recently, most measurements have concerned bulk flow variables such as the flow depth or the front velocity. Today, image processing makes it possible to visualize not only what occurs at the flow boundary (e.g., velocity profiles at the flume sidewall or free surface), but also inside the flow, allowing for a better understanding of the relations between stress and deformation rate inside moving fluids.

Combining different visualization techniques (iso-index fluids, laser fluorescence, particle tracking, etc.), we were able to measure the velocity profiles within the tip region as well as the body of fluid avalanches. In addition to these measurements (taken far from the sidewall), we also measured the flow depth profiles, front position, and particle concentrations when the flow involved dilute or moderately concentrated suspensions of particles (measuring the concentration in highly concentrated suspensions is still a challenge). Various settings were investigated: one- and two-phase flows (homogeneous fluids, particle suspensions), linear and nonlinear rheologies (Newtonian fluids, viscoplastic fluids, suspensions), laminar and turbulent regime, fixed and mobile beds, flows down an inclined flume or along a sloping bed.

The talk reviews some of the analytical results available for studying the dambreak problem. Emphasis is then given to a thorough comparison between experimental data, analytical results (lubrication theory), and numerical simulations (obtained using the shallow "water" equations) for Newtonian fluids, viscoplastic materials, and density-matched particle suspensions. We show that the front  has a specific behavior, due to a large extent to the pronounced curvature of the free surface that causes the shear stress to significantly increase (relative to the behavior in the body), but surprisingly enough, the details of this front behavior are not essential to determining the flow behavior of the fluid avalanche. The last part of the talk is devoted to avalanches of particle suspensions, whose behavior is highly dependent on the particle concentration. In spite of particle migration (which causes a significant blunting of the velocity profile), the analogy with an equivalent homogeneous Newtonian fluid performs well for concentrations as large as 0.56, but for concentrations in excess of 0.58, a more complicated behavior including stick-slip motion is observed.

Patricio BOHORQUEZ

The granular avalanche down a steep incline: ill-posedness of two-dimensional Navier-Stokes models with a mu(I)-rheology

In this talk I present the critical curve for the onset of an ill-posed regime in granular flows down an inclined plane, which is supported with direct non-linear numerical simulations. I adopt the Navier-Stokes equations with a mu(I)-rheology by Jop, Forterre and Pouliquen (Nature 44: 727–730, 2006) and consider a channel flow of infinite width with shear-stress free condition at the top. Firstly the analytical solution is developed in the presence of an arbitrary pressure p0 acting at the top. Bagnold's solution is recovered in the limit of vanishing top pressure. The neutral curve between well-posed and ill-posed regimes is derived from the ill-posedness condition by Schaeffer, Barker, Bohorquez and Gray (2014). The analytical result is corroborated with a Navier–Stokes solver (Gerris) developed by Lagrée, Staron and Popinet (J. Fluid Mech. 686: 378-408, 2011) which reproduces the developments of spurious grid-dependent instabilities. When p0 << rho g h, where rho is the grain density, g is the acceleration due to gravity and h is the granular flow depth, it is found out that Bagnold's flow is well-posed except for angles slightly above and below of atan(mu_s) and atan(mu_2), respectively. Shallow slopes remain ill-posed at all values of p_0. Conversely, steep slopes of about mu_2 becomes well-posed in the bulk of the flow at moderate pressures of the order of O(rho g h) though instabilities may arise near the top. Finally, at moderate pressures of p0 ~ O(10 rho g h) the model problem is ill-posed at all bottom slopes. These results may have important consequences for multiphase numerical models based on mu(I)-rheology where p0 represents the constant required by the pressure equation. 

François BOUCHUT

Conforming approximations of Bingham type fluid flows

We study approximations by conforming methods of the solution to variational inequalities that arise in the context of incompressible Bingham fluid flows and related viscoplastic problems, possibly without viscosity. We propose a general framework involving total variation functionals, that enables to prove convergence of time-space approximations, for time implicit, or time implicit regularized (linearized or not) algorithms. Illustrations are given for Drucker-Prager flows.

Manuel J. CASTRO

Uncertain quantification by  Multi-level Monte Carlo finite volume method: application to landslides-generated tsunamis

We present a multi-level Monte Carlo finite volume method for the two-layer Savage-Hutter model  with uncertain parameters applied to landslides-generated tsunamis. The coupled system is discretized using the first and second order IFCP (Intermediate Field Capturing Parabola) method  that is defined by using a suitable decomposition of a Roe matrix by means of a parabolic viscosity matrix that captures information of the intermediate fields. Second order is achieved by MUSCL reconstruction operator in combination with the second order TVD Runge-Kutta method.We consider uncertainty of some parameters of the model like the ratio of densities, friction between layers and Coulomb friction angle, using Multi-Level Monte Carlo (MLMC) method introduced for hyperbolic PDEs by Mishra-Schwab-Sukys. Finally, some numerical test will be shown to check the efficiency of the proposed method.

Yoël FORTERRE

Dense granular flows: toward a hydrodynamic description

Over the past decade, many progresses have been made in our understanding of the rheology of granular flows, especially in the concentrated regime that is the most relevant for geophysical applications. In this talk, I will review these advances and focus first on dry granular flows. A simple constitutive law describing the medium as a visco-plastic frictional liquid will be presented and applied on different configurations, from gravity flows to flow around solid objects. In the second part of the talk, the extension of this approach to granular material immersed in a liquid (granular suspension) will be discussed. We will see that the interstitial fluid affects the steady state rheology but can also strongly modify the transient dynamics of the flow, due to the coupling between packing fraction changes (Reynolds dilatancy) and pore pressure (Darcy flow). These concepts will be illustrated by laboratory experiments on submarine avalanches and impacts of solid objects on wet granular targets.

Daniel LE ROUX

Discrete analyses and numerical simulation of typical waves for environmental problems

The shallow-water system, obtained from the Navier-Stokes equations by vertical averaging, is extensively used in environmental studies (ocean, atmosphere, rivers) to simulate the propagation of a number of typical waves (e.g. gravity, Rossby). For most of the discretization schemes, the numerical approximation of shallow-water models is a delicate problem leading to the appearance of spurious solutions in the representation of the waves. In order to understand these difficulties and to select appropriate spatial discretization schemes, Fourier / dispersion analyses and the study of the null space of the associated discretized problems have proven beneficial. The aim of this talk is to present such results and to propose a class of possible discretization schemes, that is not affected by the spurious solutions.

Anne MANGENEY

Insight into granular collapse dynamics over inclined beds from viscoplastic modelling and laboratory experiments

Avalanches and landslides play a significant role in erosion processes at the surface of the Earth and other telluric planets. On Earth, they represent a threat for population and infrastructure in volcanic, mountainous, seismic, or coastal areas. The research field dealing with dynamic analysis of gravitational mass flows is rapidly expanding. One of its ultimate goals is to produce tools for prediction of velocity and runout extent of rapid landslides. Despite the increasing number of experimental, field and numerical studies of landslide and granular flow dynamics, the quantification of the physical processes involved such as erosion/deposition processes and the corresponding rheological behavior of both experimental and natural flows are still open questions.

We present here experimental and numerical modelling using visco-plastic models of the collapse of granular columns over inclined planes, covered or not by an erodible bed, designed to mimic erosion processes of natural flows travelling over deposits built up by earlier events.

The experiments show two different regimes, below and above a critical slope angle between 10° and 16°. For small slopes, granular flows and deposits obey established scaling laws, in particular relating the maximal runout distance to the initial column height. In that case, the flow is unaffected by the presence of an erodible bed. For slopes larger than the critical slope angle, the flow dynamics change fundamentally, with a slow propagation phase. In that case the 'classical' scaling laws are no more observed and the flow is very sensitive to the erodible bed: erosion processes can increase the maximum runout distance by up to 40% even for very thin erodible beds. Erosion efficiency is shown to strongly depend on the slope of the topography and on the thickness and state of compaction of the erodible bed.

We simulated granular collapse over inclined beds using a Drucker-Prager model based on a constant friction coefficient or on the $\mu(I)$ rheology. In the case of granular column with aspect ratio of the order of real landslide aspect ratios (<1), only very small differences are observed between the results using these two flow laws. With parameters deduced from the experiments, we show that the Drucker-Prager rheology reproduces quantitatively the experimental results on the dynamics and deposits of flows over horizontal and inclined planes. We quantify the effect of the gate on the collapse dynamics. Numerical results show that a sliding velocity is observed at the base of the flow near the front. Furthermore, zones of upward velocities, non-hydrostatic pressures and cells of negative and positive vorticity are also observed. These seemingly instabilities observed near the bottom and under the flowing region may have a key role in erosion processes.

Guillaume OVARLEZ

Suspensions of particles in yield stress fluids: macroscopic behavior, and shear-induced inhomogeneities

Many dense suspensions involved in natural phenomena (debris-flows, lava flows, etc.) and industrial processes (concrete casting, drilling muds, etc.) are yield stress fluids which contain a significant fraction of coarse rigid particles. When scale separation between the paste microstructure (the colloidal particle size) and the noncolloidal particles in suspension is possible, a simplification occurs: these materials can be considered as noncolloidal particles embedded in a yield stress fluid (the colloidal paste). From a fundamental point of view, one then deals with suspensions in which particles interact through nonlinear hydrodynamical interactions.

In this talk, we will present recent advances in the characterization and understanding of the behavior of suspensions of rigid inclusions in yield stress fluids. We will first focus on the impact of the noncolloidal particles on the linear and nonlinear rheological properties (elastic modulus, yield stress, apparent viscosity) of the fluid. We will show that the variations of these properties with the particle volume fraction observed experimentally are in good agreement with those predicted by a micromechanical approach in which the concentration of shear between the inclusions is taken into account. We will also deal with microstructural aspects. We will show that an anisotropic microstructure is developed under shear. This microstructure depends on shear history; at a macroscopic scale, a shear history dependent behavior then emerges due to the presence of particles. In particular, these observations provide a mechanism for strain hardening in reinforced materials.

We will also discuss sedimentation issues. Although dense particles can be stabilized at rest in a suspension when the interstitial paste has a high enough yield stress, we will show that sedimentation is induced as soon as the material is sheared. This phenomenon of shear-induced sedimentation can be quantitatively understood when the 3D behavior of the interstitial yield stress fluid and the local properties of shear between the particles are taken into account. We will finally discuss briefly shear-induced inhomogeneities, which are observed even when the density of the particles and the fluid are matched. A diphasic description of the suspensions attributes this shear-induced migration process to the gradients of the normal stresses exerted on the particle phase alone. Comparison between the experimental results and the theory shows that this description still needs to be improved.

Vladimir SHELUKHIN

Cosserat-Bingham Fluids

 We consider Cosserat-Bingham fluid  which is both a micropolar medium  and a viscoplastic material. On one hand, such a fluid exhibits microrotational effects and microrotational inertia; the fluid can support the couple stress, the body couples and the nonsymmetric stress tensor. On the other hand, the fluid stiffens if its local stresses and local couple stresses do not exceed some yield stress tau_* and a yield couple-stress tau_n respectively.
We are mainly interested in incompressible fluids, but nevertheless we will also discuss the general situation.

We focus on constitutive laws for the micropolar non-Newtonian fluids which can support yield stresses. Such fluids include animal blood, cutting transport by drilling mud, and granular flows. In mechanics of the classical Bingham fluid, there is only one yield stress tau_* because the local stress state  is characterized completely by only one tensor; it is the Cauchy stress tensor T. To characterize stresses in   the micropolar fluid, one should take into account the couple stress tensor N also; this is why we incorporate a yield couple-stress tau_n. As for local deformations, they are  characterized also by two tensors which allow to calculate the velocity gradient and the spin gradient; both these tensors should vanish in the zone of stiffness, the strong plug zone. In contrast to the classical Bingham fluid, the micropolar Bingham fluid may have a weak plug zone where the spin gradient vanishes whereas the velocity gradient does not vanish. We give examples of flows with weak plug zones.

We restrict ourselves to a simple micropolar viscoplastic fluid. The corresponding constitutive equations require a minimal number of viscosity coefficients. To illustrate the equations derived, we consider shear flows between two parallel planes. We show that the apparent viscosity increases as the canal thickness decreases in agreement with the inverse Fahraeus-Lindquist effect  for the blood seepage through a narrow capillary tubes at high values of hematocrit. Observe that, within the Cosserat-Bingham approach, there is no flows for low values of the canal  thickness.  As for applications in transport of drilling cuttings, the model developed here predicts that even small increase of the drilling mud discharge may result in a significant pressure growth within the borehole if the cutting concentration and the mud composition are such that the rotation viscosities, corresponding to  the mud-cutting mixture, are not negligible. The borehole pressure control is of great importance in the well stability problem.

We also address the question of solvability of the derived equations.

Paul VIGNEAUX

Numerical schemes for viscoplastic shallow flows with wet/dry fronts

In this talk, we describe the numerical resolution of a shallow water viscoplastic flow model. Viscoplastic materials are characterized by the existence of a yield stress: below a certain critical threshold in the imposed stress, there is no deformation and the material behaves like a rigid solid, but when that yield value is exceeded, the material flows like a fluid. In the context of avalanches, it means that after going down a slope, the material can stop and its free surface has a non-trivial shape, as opposed to the case of water (Newtonian fluid). The model involves variational inequalities associated with the yield threshold: finite-volume schemes are used together with duality methods (namely Augmented Lagrangian and Bermudez-Moreno) to discretize the problem. To be able to accurately simulate the stopping behaviour of the avalanche, new schemes need to be designed, involving the classical notion of well-balancing. In the present context, it needs to be extended to take into account the viscoplastic nature of the material as well as general bottoms with wet/dry fronts which are encountered in geophysical geometries. This is a joint work with E. D. Fernandez-Nieto and J. M. Gallardo.

 _____________________________________________________________________ 

How to come ?

The IMUS' Building is located on the Reina Mercedes Scientific Campus in the south part of Seville (ask for "Avenida Reina Mercedes").

The following maps gives you a physical overview of the entrance : open maps.

The workshop's room is on the first floor.

Exact coordinates and bus information are here.